Around the World, and Back

The Travelling Salesman Problem (TSP) is a graph theory problem that requires the most efficient, i.e. shortest, closed-loop path through which a salesman can travel to each of n cities, exactly once [1]. Such a loop is called a Hamiltonian cycle [2] and there is no known general solution to the TSP. Practical applications to the solution of the TSP include the scheduling of tasks on a computer and ordering of genome features [3]. Inspired by the last example on this page, I tried projecting the shortest path through every country on the planet and visualising it on a map. To do this, I used the FindShortestTour function, which tries to find the shortest path through all the countries—going through each country once.

I used the following code to gather the names of the countries in the world and to find the shortest path going through the centre of each country.

Copy 
1c = CountryData["Countries"];
2geocen = Map[CountryData[#, "CenterCoordinates"] &, c];
3{dis, path} = FindShortestTour[geocen];

Next, I visualised the results on a map using the following code.

Copy 
1Export["mapflat.svg",
2  GeoGraphics[{
3    FaceForm[White],
4    EdgeForm[{Thin, Gray}],
5    Polygon[c],
6    GeoPath[c[[path[[1 ;; Length@c]]]]]
7  }, GeoRange -> "World", GeoBackground -> None, ImageSize -> 700]
8]

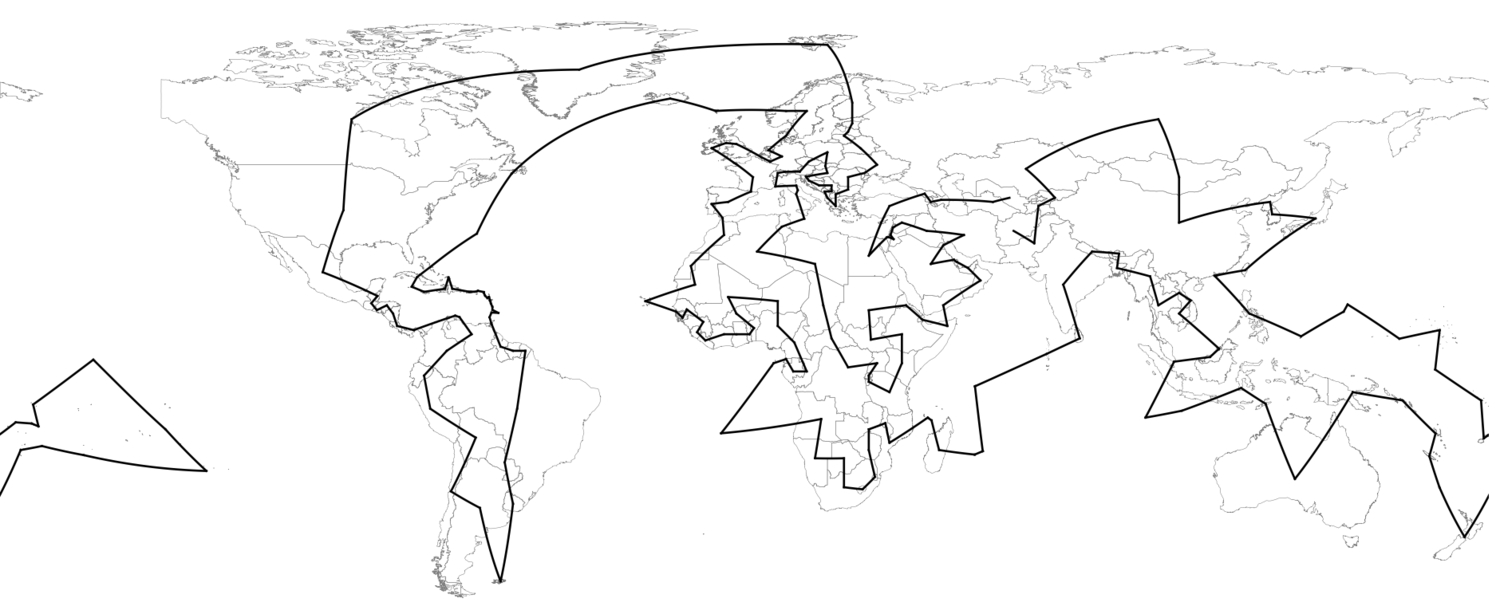
To view the path using an orthographic projection:

Copy 
1GeoGraphics[{
2  FaceForm[White], EdgeForm[{Thin, Gray}], Polygon[c],
3  GeoPath[c[[path[[1 ;; Length@c]]]]]},
4  GeoRange -> "World",
5  GeoProjection -> {"Orthographic", "Centering" -> CountryData["World", "CenterCoordinates"]},
6  GeoBackground -> None, ImageSize -> 700]

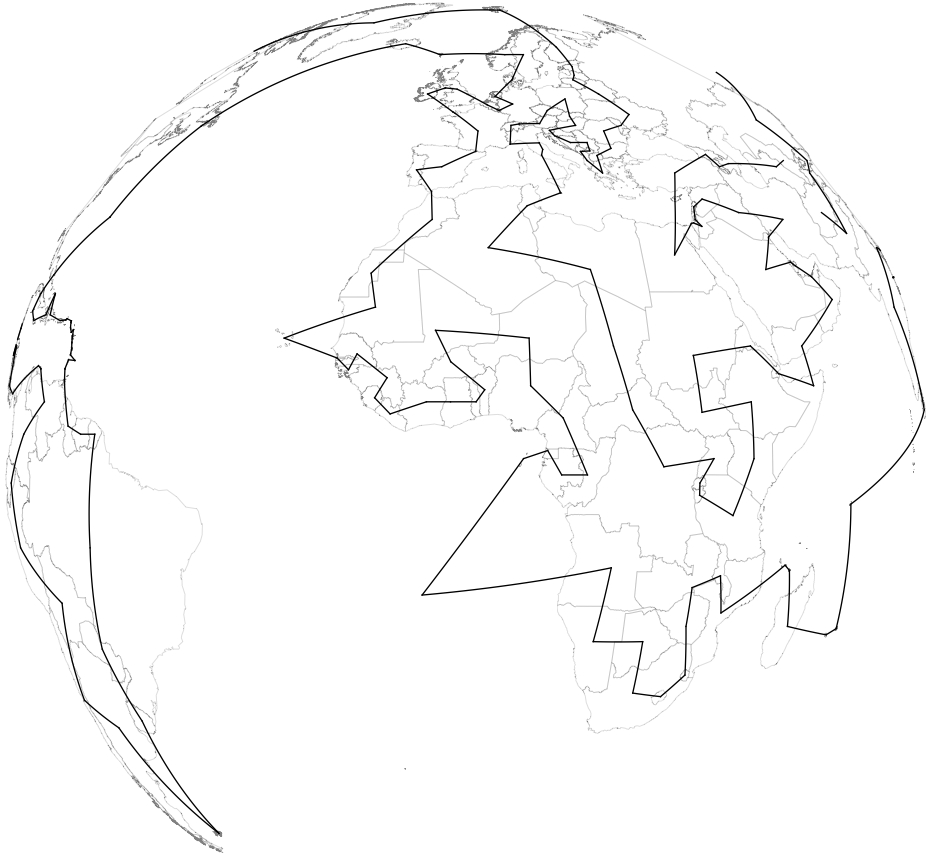
I then created an animation of the travelling salesman going around the globe.

Copy 
1Export["animation.gif",
2    GeoGraphics[{GeoStyling[FaceForm[White], EdgeForm[{Thin, Gray}]], Polygon[CountryData["Countries"]], GeoStyling[FaceForm[Orange]], Polygon[c[[path[[#]]]]], {Gray, GeoPath[geocen[[path[[1 ;; #]]]]]}},
3     GeoRange -> "World", GeoProjection -> {"Orthographic", "Centering" -> geocen[[path[[#]]]]}, GeoBackground -> None, ImageSize -> 300] & /@ Range@(c+1),
4 ImageResolution -> 300, "DisplayDurations" -> 1.5]

As the travelling salesman moves to the next country, the centre of projection also moves to that country. The animation begins with Afghanistan because the list of countries CountryData["Countries"] returned was arranged in alphabetical order. Bear in mind that this is an attempt at finding the shortest path, going through the geographic centre of each country, which results in a distance of about 112,312 miles. This distance can be reduced in a few ways -- taking a different route for instance, or, starting from a different country.

— MS

[1] Weisstein, Eric W. "Traveling Salesman Problem." MathWorld.

[2] Weisstein, Eric W. "Hamiltonian Cycle." MathWorld.

[3] Erica Klarreich (2013)