Wolfram Notebooks

This article was originally written as an exploratory note here.

I use Wolfram Notebooks almost daily. Over the past few years, it's become a medium for thinking, exploring and documenting ideas, beyond just coding. Here, I'll share some of my thoughts on using Wolfram Notebooks and why I find them useful as a thought medium.

CAS to code

Notebooks—in the computational sense—date back to the '80s. Back then, notebooks primarily served as interfaces for the long-established Computer Algebra Systems (CASs). As the name suggests, a CAS is a software used for carrying out mathematical computations. CASs typically have an interface for visualisation and a programming language for scripting computations.

One such system was the Symbolic Manipulation Program (SMP), which later developed into Mathematica. Mathematica 1.0 was launched on June 23, 1988. While maintaining its familiar façade, Mathematica has continuously advanced since then. It has gradually transcended from being a CAS to a general-purpose programming tool. You can do mind-blowing physics, and then create a website to showcase your findings, within the same session. Such scope is non-existent amongst CASs.

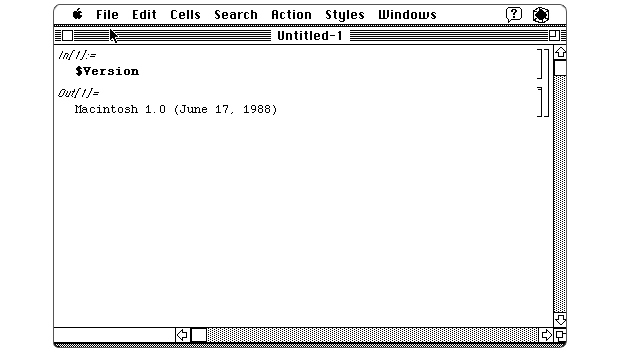
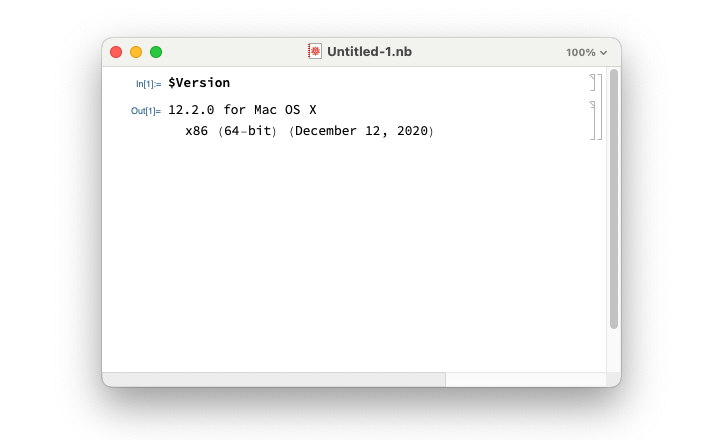
Simpler though it was, Mathematica 1.0 had a similar interface to its latest version, 12.2. The layout is identical: a sequence of inputs and outputs, linked and grouped by cells. Also, the programming language has been very consistent. While all kinds of improvements have been made over time, a lot of things have remained the same—V1 code still works in V12.

For example, the interface now predicts what computation one could be thinking of, or what one might want to do next with an output. It can handle sounds and images (not to be confused with plots—1.0 very well supported plots), and hundreds of other data formats. What's more, one can run computations directly on cloud servers, which weren't a thing back then. Nonetheless, getting the first one thousand digits of $π$ is still the same: N[Pi,1000], perhaps faster now.

For a long time, the term Mathematica referred to CAS, interface (notebook) and symbolic language. That trinity no longer holds today, as the system has now been divided into different products: think of Wolfram Mathematica as a CAS,Realistically, Mathematica is more than just a CAS. As I'll show later on, the kinds of computations it is capable of performing greatly exceeds the scope of a standard CAS. Wolfram Notebook as its interface, and the Wolfram Language as a symbolic language for writing and manipulating computations in that CAS.

The history of CASs and how their incipiently rudimentary displays evolved into modern computational notebooks for interacting with them is interesting.Kajler & Soiffer (1998) cover the early history of CAS interfaces. But here, I'll focus on modern Wolfram Notebooks. It is possible to discuss Wolfram Notebooks without centring on the Wolfram Language because you can use them to do serious programming in other languages (JavaScript, Julia, Python, R Ruby, and SQL). However, you get the full functionality of Wolfram Notebooks using the Wolfram Language, so I'll discuss them in tandem.

Coding

Think of a Wolfram Notebook, firstly, simply as a tool for writing and executing code. Now, how does one write code? You would normally type it, and often copy and paste it.

You type something in, you get something out: 9 * 8 gives 72. Depending on the environment you're coding in, you may receive prompts whenever a result is returned or an error is raised, and nudges if the environment has a suggestion for you, this could be an annotation to a printed result, or a heads-up to prevent you from making an error.

We encode or program computations following specific rules, and each programming language has its own. You probably would write $9 × 8$ if doing so on a piece of paper. But with most languages, you need the asterisk. And that's one of the simplest differences between how one might think on paper, as compared to in an IDE.

A Mathematica notebook is less a record of the user’s calculations than a transcript of their conversation with a polymathic oracle.

— James Somers, The Scientific Paper Is Obsolete

But is writing, enumerating, listing, sketching—and all those other things we use the paper medium for—the same as thinking? Not quite, they are expressions of thoughts. (I'm inclined to think it is, though I don't know, and I will be finding out soon.)

Another way of looking at the Wolfram Notebook is as an intelligent, digital version of the good old notebook. It is intelligent, in that, it is "able to vary its state or action in response to varying situations." (See definition.) And this sets it apart from most other programming languages. I will explain why I think so, starting with $9 × 8$.

When you type 9 and 8 separated with a space, it's automatically converted to a ×. It only does this for numbers, though it still multiplies things that are separated by whitespace. Free-form input creates room for improvisation, thereby extending one's imagination. This is how it works: you type in anything—anything at all—and it tries to make sense of it, and give a response. It doesn't always conjure up the expected interpretation. It sometimes fails to interpret what would seem obvious to a child. However, it encourages creativity, especially in children. And it amuses them. I will tell you more about that later.

Here are other ways to input code or more generally, expressions, in a Wolfram Notebook:

Writing

From the notebook above, it is immediately clear that inputs can be versatile, interpretable and systematic. Notebooks also serve as documents, and they can be used for formal writing. For example, this is a monograph-styled notebook template.

But is all this the same as writing? Well, yes, in the digital sense—just like one would use a Word or Markdown document to write. But not in the traditional sense—pencil on paper. Digital and analogue forms of writing both have their advantages and limitations, though they are increasingly becoming dissimilar in act. Think Apple Pencil. Certainly, it is of immense creative benefit. But what influence, if any, does this dynamic form of writing have on the way we think?

Drawing

How about drawing? I prefer the analogue form of drawing, but which is better is a matter of opinion. One artist might say that drawing with a stylus on a glass pane doesn't feel as natural or as dynamic, as compared to using a pencil on paper. Another might appreciate its fluidity and the ease of correcting mistakes. Nonetheless, both the iPad and the drawing paper provide a medium for boundless artistic expression.

The Wolfram Notebook allows you to draw on a graphics object called Canvas. Clicking the canvas displays a variety of drawing tools. You can draw lines, arrows, polygons and so on. It allows you to draw freehand too. You can add preset shapes, and text and equation boxes onto the canvas. There are options for editing and styling each object to your liking.

You can select graphical elements from a canvas and compute other things with them. In the notebook above, I picked the red triangle and added a hatch filling to it. I then replaced the hatch pattern with the "hello" I'd drawn.

Seeing and hearing

Amongst programming languages, the Wolfram Language has some of the most advanced plotting and visualisation functionalities, and the Wolfram Notebook takes full advantage of this. It enables one to see things with great insight and clarity. By "things", I mean data, mathematical functions, pictures and videos, colours, cities and countries, the human anatomy, and many more. Abstract concepts are easier to navigate and understand inside of a Wolfram Notebook because they can be made visible, and interactive. You can play an animated image (GIF) or a video inside a notebook.

Let's consider a simple but practical example. Fọláṣadé resides in Lagos, Nigeria. That bustling city! It's Friday, the fifth of June, and she's out with a friend, let's say they're at a park. She's lying on the grass, gazing at the vast blue sky. Lagos is very warm for most of the year and that day was a tad sultry. She spots a plane heading eastwards and follows it until it vanishes into a big cloud. Fọláṣadé then begins to wonder, about the planets, stars and constellations.

Let's step back into the notebook for a moment. One can visualise the sky and see where celestial objects are whether it's night or daytime. Maybe, like Fọláṣadé, you are curious to know where the planets are in relation to one another. Using inbuilt functions and external ones created by a growing community of Wolfram Language users, you can also see the solar system and even the Milky Way galaxy. People use notebooks to keep track of rare events such as eclipses or travel back in time to learn a bit of history about manned space missions.

Now, back to Lagos. You can see below what the Lagos sky looked like at midday on that day. (Can you spot Sirius?) The sun was up and nearly aligned with Venus, Mercury and Mars (at the right edge; barely visible in the image). Although Ṣadé most probably could not see the planets that afternoon. Besides, the glare of the sun is best avoided.

What could the park have sounded like? We could imagine that it was lively and people were having a good time. The first audio simulates what the park might have sounded like—indistinct chatter of residents and tourists, the flapping wings of pigeons, leaves rustling against themselves, the laughter of children and perhaps distant music, or the fading roar of an airplane. That airplane. Using actual weather data of Lagos on that very day, we could model the attenuated sound that could have been audible, say, 10 meters away from the source of the first audio. This is a practical example of how one could see and hear more of the world around them in a Wolfram Notebook.

Of course, visualisations and computationally modelled sounds are no substitutes for—and are incomparable to—the rawness of reality. But for a young and inquisitive girl or boy, these are invaluable tools for gaining deeper insight into the world around her or him. And what a fun way to do it. To be able to see and hear and speak and ask and touch and drag and drop and slide... and chat and share the fun with others.

Exploring, ideating and imagining

The unique coding, writing and drawing capabilities of the Wolfram Notebook—combined with its audiovisual interactivity and receptivity to input of human and machine expressions—makes it apt for exploring ideas. The variety of ideas that one could explore in a notebook is so vast, that the notebook becomes a sort of encyclopaedia. Apart from making software, Wolfram Research is also into the business of curating information and making it computable. Thus far, the areas of knowledge they've covered range from food and nutrition, to art and design, to weather and meteorology.

Being able to compute things on a whim with so much meaningful up to date data about the world, gives fluidity to the process of creating and exploring ideas in a Wolfram Notebook. As you've seen in previous examples, you can retrieve appropriately quantified data on your surroundings, with some degree of precision as regards space and time. With Entities, the world and everyday life become even more computationally explorable.

So what, if so many things can be computed (with)? Why should you care, and how useful is any of this? I'll give you three reasons:

1. Because you can solve real-life problems in ways that make the path from problem to solution less abstract and clearer. For first, you have near real-time data readily available. Whether the nature of the data is transient (as in weather and financial data), long-lasting (as in socioeconomic and demographic data), or immutable (as in mathematical, chemistry and physics data). But it doesn't end with the data, you can use it in meaningful ways too.

2. Apart from problem-solving, we are sometimes simply curious to figure out interesting facts and relations about the world. Whether it's a book you're reading or a tender plant you're looking after, knowing about the world at your fingertips accelerates the fulfilment of curiosity and learning.

3. The world and how we interact with it and one another, is increasingly becoming computational.

So, I think you should care, because here is a tool that can facilitate and enhance your modi operandi for exploring, ideating and imagining. You can see examples of exploratory data analyses I have used notebooks for here, here and here.

While the predictive interface as a whole allows you to write and iterate through code quicker, the Suggestions Bar encourages asking "what if" questions—it invites you to see what more you can do with—or learn from—a result, be it a number, word, colour, entity, date or a more complex object. Try evaluating each of these in the notebook below and see the suggestions that come up: Pi, "Sunset", ColorData["SunsetColors"], Entity["Star", "Sun"], Sunset[]. Click on the ⊕ icon to see additional input options.

There are thousands of functions—querying the number of all functions (Length@WolframLanguageData[]) gives $5,826$, but there are certainly many more functions that are undocumented. How does one remember them all?! One simply can't, but as with any language, over time, one builds memory of the names of things, and intuition for guessing the name of a thing that one doesn't know or can't recall. There are two attributes which make the names of Wolfram Language functions easier to recall or correctly suppose: using natural language, and consistent naming and documentation.

First, you code using natural language—in English, or with code captions for other languages. This means using everyday words to do and create things. Here's a basic example: you have a list, called things, and you want the first and last items in it; you simply say First[things] and Last[things]. Similary, Today means today. There are countless such cases whereby a word really, unambiguously does or renders the thing it means. And the computation, or the result, needn't necessarily be trivial, even if the input looks so simple. Here's another example, this time of Integrate integrating $\mathrm {sech(\mathnormal{x})}$ Integrate[Sech[x],x], which gives $2 \arctan \Bigl( \tanh \Bigl( \cfrac x 2 \Bigr) \Bigr)$.

Not all functions are single-worded, there are many functions whose names contain two or more words adjoined. This brings me to the second attribute: consistency. For what it's worth, the Wolfram Language has one of the most consistent naming and documentation systems amongst programming languages. Take a look for yourself, it spans decades—Version 1 code from 1988 still works in Version 12.2 (released December 2020). Here's Stephen Wolfram doing a demo of V1 and V12.2, three decades apart.

Let's consider making plots and charts. There are various kinds of plots and charts, and a function for each kind. But they all end with Plot/Chart, or Plot3D/Chart3D for the three-dimensional variants. There are exceptions such as Histogram, but this is perfectly reasonable because that's what it's commonly called. The same thing applies to many other groupings of functions, such as those for geo-computation, which have the prefix Geo; or functions for getting data, which are suffixed with Data.

A combination of such exceptional consistency and using natural language makes it easier to guess what a function might be called, even though there are thousands of functions.

Learning and teaching

I have the privilege of teaching kids and adults programming, using Jupyter Notebooks for Python and the object of interest for Wolfram Language. In my two and half years of doing this, I have realised the extent to which the framework provided for thinking about an activity or problem—and engaging in it, or attempting to solve it—can influence the way one approaches the problem.

For instance, consider geometry as taught in primary and secondary schools. Textbooks try, but I think a better way of teaching geometry (and many other topics) is by using a computational notebook. Possibly true for other topics, but particularly for learning geometry, the traditional textbook is limited in many ways. Firstly, can present and visualise only a single instance of a problem at a time. The issue with this isn't that copious space is needed to show an ample variety of possible scenarios to better the learner's understanding. Rather, the issue is that each explanation, each example, each exercise, is static and therefore, potentially limiting. By this, I mean that the static setting puts a ceiling on the knowledge and intuition the student gains from the process of following an example or solving an exercise. By contrast, a dynamic/interactive setting allows the student to view the scenario from different vantage points. Apart from visualisation and feedback, another benefit to this is that the student begins to ask "what if...?"; the Suggestions Bar encourages asking such questions. The second point is more of a personal opinion: it is often uninspiring.

I believe what learners of topics such as geometry (and indeed the subject of mathematics itself) need, is a medium in which the learner can see how angles, dimensions, shapes, volumes—objects and entire scenarios—morph as they interact with the geometric elements. Be it by writing, typing, drawing, clicking or dragging, immediate feedback of the learner's actions and ideas will greatly enhance learning and the development of the learner's intuition of the underlying principles which those scenarios aim to elucidate. It may also allow the student to learn underlying principles and build intuition quicker.

Let's take a look at one such scenario. In the notebook below we have a 2-dimensional geometric setting (GeometricScene). It contains the following geometric objects and assertions:

1. there are two similar triangles ($\textcolor{#9ca5a6}{\triangle abc}$ and $\textcolor{#f29494}{\triangle bcd}$) enclosed by a $\textcolor{#50b050}{\mathrm {circle}}$
2. $\measuredangle bac = 90 \degree$ and $\measuredangle bcd = 45 \degree$
3. an $\textcolor{#fd7400}{\mathrm {infinite~line}}$ passes through points $\textcolor{#1c69ee}{\bm a}$ and $\textcolor{#1c69ee}{\bm d}$, and another $\textcolor{#6b1fb1}{\mathrm {infinite~line}}$ passes through point $\textcolor{#1c69ee}{\bm c}$ and a point $\textcolor{#1c69ee}{\bm e}$ on the $\textcolor{#50b050}{\mathrm {circle}}$

The scene is interactive and updates (within the established constraints) as you click and move the points around and points can be pinned to specific positions. I believe this is a more interesting way of presenting a geometry problem to a student. I do not think that the interactivity might be a distraction. Rather, it allows the learner to take a deeper look into the problem. For example, we can ask for geometric conjectures that can be derived from this particular scene, and highlight them. The second scene highlights $\angle bac = \angle cbd = \angle dca = 90 \degree$, but there are many others as you can see in the table.

The geometric scene not only helps the learner with insight, but it can also help students learn geometric construction. For example, a teacher can put together a sequence of steps for students to follow. While this is unlike using a ruler and a pair of compasses, it is still apt for teaching. Besides, the digital medium has its benefits. For instance, when explaining a theorem such as Kosnita's Theorem, which consists of many geometric objects, the paper medium is not as apt as an interactive one.

Interactivity is particularly advantageous here. Plus, being able to pin a point and move the diagram around it is also very useful when trying to understand how the theorem works. Compare that to the static diagram sourced from Wikipedia. The diagram is neat, but the learner cannot use it to see how the blue lines remain concurrent as points move about. Here's another excellent interactive example of the theorem.

To further demonstrate the efficacy of Wolfram Notebooks for learning and teaching, I refer you to two sets of resources:

1. Wolfram Demonstrations: these are interactive interfaces that explain how things work—from maths to creative arts to everyday life. Whatever you're curious about, there's probably a demonstration on it or related to it. You will find many interesting things on there and you can interact with demos in a cloud notebook.

2. Notebook Archive: this is a collection of books, computational essays, courses and many more, all written in Wolfram Notebooks This video shows how to create a lecture notebook.

3. Documentation: contains detailed explanations of all functions including examples, how-to's, workflows, etc. Here's a summary of previous releases.

Shortcomings

• Accessibility: the Wolfram Notebook is most accessible online, though it is (understandably) limited in its functionality compared to the desktop version. This means that some important capabilities such as canvas and geometric scene are either not (yet) functional, while some others are limited. I hope that notebooks will continue to be accessible long-term, that is, without requiring signing up.
  
  

  [Update: As of November 2021, an account is needed to use a notebook online.]

• Performance: even on the desktop, the frontend often lags when handling more complex tasks. This occurs especially when dealing with graphics objects. Sometimes, the only solution is to quit and relaunch the application.

• Correctness and validation: besides bugs, which are inevitable in any worthwhile software product, there's a history of complaints regarding the incorrectness of some results of Wolfram code. Follow, for example, Richard Fateman's lecture. He gave that lecture back in 1993. Incorrectness is still an issue today. Although I've seen some examples in plotting/graphics, it seems that most of the incorrectness complaints come from people who do numerical computations a lot.
  
  

  Because the core of Wolfram Notebooks is proprietary technology, it isn't open to inspection by the public. This has frustrated many researchers (including Economics Nobel laureate, Paul Romer), though others continue to forbear deserting Wolfram Language for open-source alternatives.
  
  

  Perhaps this issue particularly irks staunch (or those who once were) users of Wolfram notebooks, because they enjoy using the product and have formed an affinity with it. They want it to be better—being more open is one way of achieving that. Wolfram Research Inc. (WRI), on the other hand, has other ideas. Business ideas. WRI has taken great pains to explain—in speech and writing—why Wolfram technology isn't open source.
  
  

  They have some good reasons. I find a few flimsy though. Here's one:

  1. They claim that "open source doesn’t bring major tech innovation to market."
  2. But build the machine learning backend of the Wolfram Language using the open-source deep learning framework Apache MXNet.
  3. Then they say that "Wolfram has pioneered highly automated machine learning—and deeply integrated it into the Wolfram Language...".

  That sounds like open-source (MXNet) bringing major tech innovation (ML automation) to market. Open-source software and tools power many of the amazing tech we enjoy today but often do so quietly. Wolfram has a page full of open materials. The Function Repository allows anyone to add to the thousands of pre-existing functions in the Wolfram Language, or even provide alternatives to them. Maybe in the long-term, this will lead to not just an equilibrium between WRI and avid users of its software, but a symbiosis.

You can read the Cloud release notes here, as well as additional implementation notes here. If you're looking to use the Wolfram Cloud long-term, you may find it useful to refer to these notes from time to time.

Interesting users/uses

In addition to the resources I've mentioned, the following are some other interesting uses and users (at least, to me) of Wolfram notebooks:

• Emerald Cloud Labs allows you to create, run, explore and analyse experiments remotely using Wolfram Notebooks. The lab is mostly run by robots. This is one of a large number of organizations—small and large (from universities to NASA and CERN)—that use it.

• Nassim Nicholas Taleb uses Mathematica extensively. Here's an example. He was awarded a Wolfram Innovator Award in 2018. (Needless to say, other recipients of the award have used Wolfram Notebooks in fascinating ways.)

Thanks to Stephen Dogo and Udeme Udoyen for reading a draft of this note.

Header image from Wolfram Research.