Topological Data Analysis for Misinformation Detection

I'm currently a researcher focusing on detecting misinformation using machine learning. This is an idea I had this summer. I've sporadically been reading on TDA for some time, and I'm intrigued by its applications in data science and machine learning, especially on high-dimensional data. I'm not an expert on TDA, but I hope to explain the viability of using it for mis-/disinformation analysis detection in this note.

Topological Data Analysis

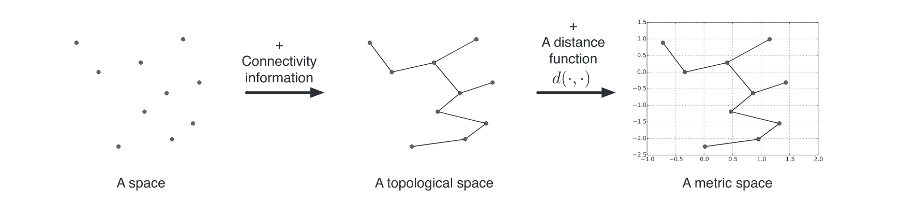
Topological Data Analysis (TDA) derives from topology, which is a branch of mathematics that studies spaces and their qualities. It is an emerging application of the concepts of algebraic topology towards understanding high-dimensional data [1]. The fundamental premise of TDA is that “data has shape and shape has meaning” (Ayasdi, n.d.). Therefore, shapes extracted from the data can quantitatively and qualitatively summarise it. This is achieved by quantifying the geometric properties of topological features (such as cycles, holes and voids) of that dataset. Figure 1 shows a simplified transformation of data into different kinds of spaces. TDA is being used to solve increasingly diverse real-world problems [2], [3], and more recently, together with machine learning [4]–[6].

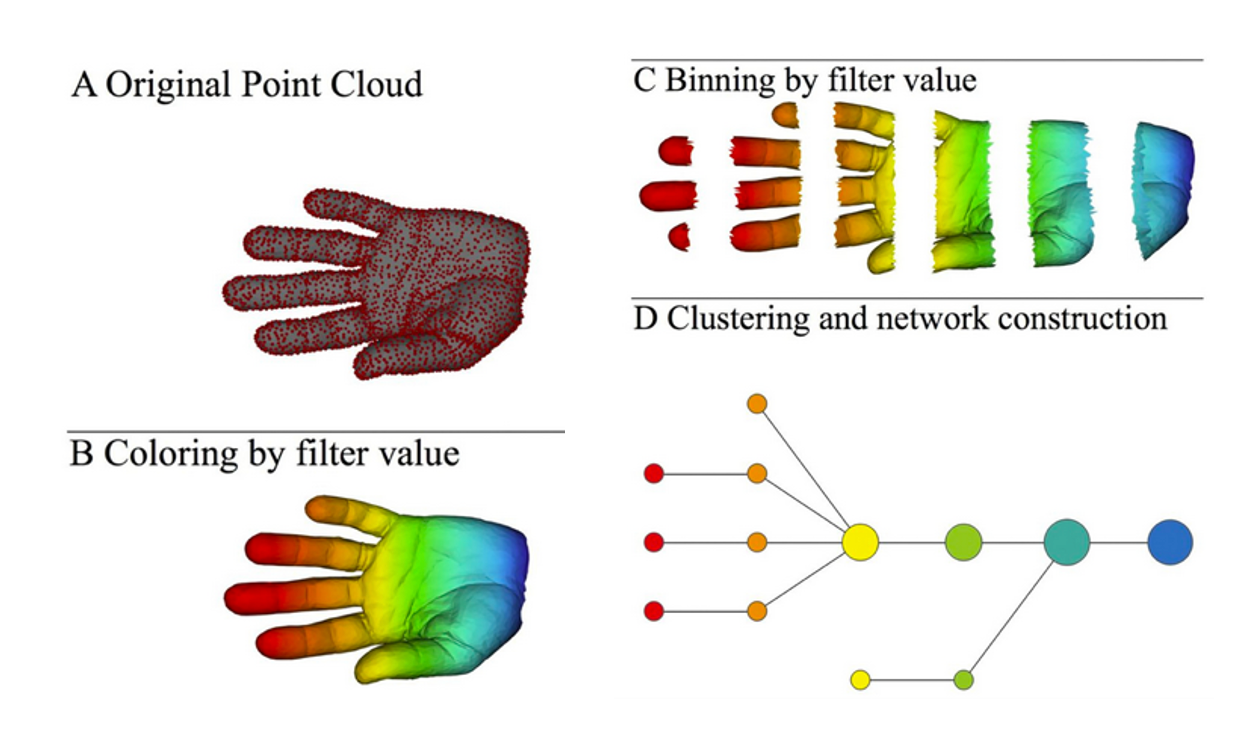
TDA is commonly implemented using two methods called persistent homology [8] and mapper [9]. In persistent homology, the main topological structures of a dataset are found using simplicial complexes (see Figure 2). It aims to measure the longevity of topological properties of a simplicial complex when simplices are removed from or added to it [10]. Extracted topological features can be represented using visualisation tools such as persistence diagrams, persistence barcodes and persistence landscapes [11]. The output of mapper is extracted patterns in a high-dimensional dataset in the form of a graph, rather than a set of points (see Figure 3). TDA will be discussed here with a focus on mapper because it is more straightforward to implement and mathematically simpler. The application of mapper to a high-dimensional dataset $X$ can be summarised into the following steps [1]:

1. A filter function f is applied on $X$ and filter values are saved. This function assigns a real value for each data point in $X$.

2. The range of filter values is subdivided in $k$ overlapping intervals.

3. For each interval, data points in $X$ that correspond to that interval are clustered together. This clustering is done for each interval, giving $k$ clusters.

4. Following clustering, a graph is created with vertices representing each cluster. Because the filter intervals are overlapping, a data point in $X$ can appear in two clusters. If any two clusters contain at least one data point in common, then an edge is drawn between the vertices which represent those two clusters.

Additionally, a colour function based on the filter values or the properties of data points that constitute a vertex can be applied to the graph for visualisation purposes.

The caveats of using mapper are that: i.) its outputs are highly sensitive to the filter function used; ii.) the overlap between filter intervals; iii.) the clustering method and distance function used. Nonetheless, its low-dimensional output still normally effectively captures the patterns in the high-dimensional input data.

Why TDA?

TDA has been proven to be effective in scenarios whereby higher-order interactions exist; it is capable of capturing the global topology of that system to reveal the system’s intrinsic structure [12]. It can detect small and large scale patterns that normally elude other methods such as multidimensional scaling (MDS) or principal component analysis (PCA) [2].

These are some of the reasons why TDA is effective [2]:

• Coordinate invariance: The constructions that result from topological methods do not depend on a chosen coordinate system but rather, on the distance function that specifies the shape. The constructions are not affected by a change of coordinate systems or shape rotations because they are based on a metric space.

• Deformation invariance: Topology captures shapes that are invariant under minor deformations. This makes it a lot less sensitive to noise and reduces the need for pre-processing.

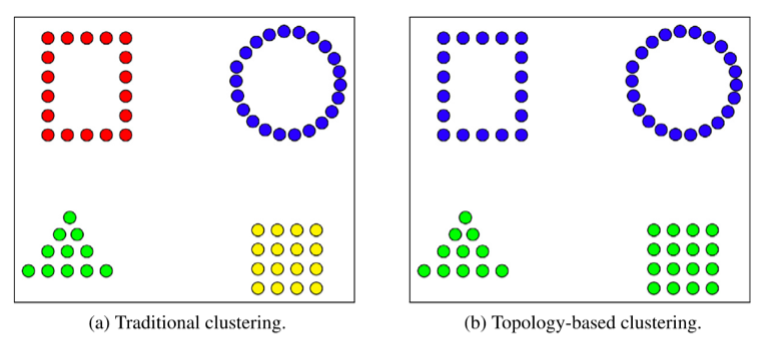
• Compressed representation of shapes. TDA is great for creating simple yet insightful representations of high-dimensional data. As opposed to multidimensional scaling whereby a cluster of similar data points can be hidden behind another cluster, TDA represents entire clusters as a vertex on a graph.

Applicability to fake news detection

The multi-faceted nature of disinformation—falsity in text, speed of dissemination, bad actors, et cetera—makes it a very challenging problem to solve. It is also a dynamic problem as bad actors are continuously adapting to evade established fake news detection techniques. TDA is ideal for uncovering hidden patterns in complex systems and processes [13]. This makes it apt for understanding and detecting fake news networks and dissemination.

In reality, many news articles cannot be explicitly categorised as “fake” or “real” because they contain elements of both truthiness and falsity in differing proportions. For example, an article may contain a factual paragraph that introduces a real-world event. What follows could be an erroneous discussion of the said event. supported with false claims. This adds to the difficulty of spotting high-level patterns in fake news datasets.

TDA is effective for studying noisy high-dimensional data such as fake news datasets, extracting their fundamental shape or structure and acquiring qualitative insights from them [14]. Because it has the potential of finding shapes that are persistently unique to fake and real news, it allows for a better-informed approach towards selecting features of fake news detection based on those differences. Finally, TDA works in an unsupervised way.

Improvements TDA offers

Some fake news datasets are multi-domain, meaning they contain news on different themes such as politics, entertainment, sports, etc. The attributes of fake entertainment news, for instance, may be somewhat different to those of politics. This makes clustering on multi-domain datasets more difficult. With TDA, clustering is an intermediate step rather than the final one. It is applied to multiple subsets of the data and the final output can be a connected graph rather than a set of points. Connectivity—coupled with the ability to apply a colouring function onto such a graph—could make the interrelationships between different subtypes of authentic and fake news may be more apparent. TDA offers the potential to capture the similarities and differences between fake and real news of different domains.

Furthermore, the authenticity of articles is a continuous property rather than a discrete one. Traditional clustering methods work based on the assumption that the clusters are coherent. However, with misinformation, the clusters formed by fake and real news are not highly coherent—their boundaries are not well defined and intersect. In the case of mapper, for example, edges on the graph can be cut as opposed to drawing a line through clusters of points.

Potential challenges and mitigations

• Speed and expense of computation: computing persistent homology is expensive [15]. However, it is less so for mapper. There are libraries such as giotto-tda and Topology ToolKit, which claim to be fast and efficient for TDA computations.

• Finding good filter functions: Filter functions can be statistical (mean, max, variance, etc.), geometric (centrality, curvature, harmonic cycles, etc.), machine learning (PCA, MDS, Autoencoders, etc.) or data-driven (linguistic features) [16]. Finding good filter functions is usually done iteratively as a good filter can be application domain-specific.

• Other parameters: with mapper, for example, some parameters that influence its performance. Carrière et al., 2018 thoroughly analysed these parameters and came up with a robust framework for automatically tuning them.

Examples

TDA pipeline

The following steps form a potential pipeline for fake news detection using persistent homology:

• Data input
  • Raw news data (text, timestamp, source, social network data, …)
  • Data cleaning/preparation (remove stopwords, …)
  • Embed data into point clouds
• Persistent homology
  • Construct simplicial complexes (e.g., Vietoris-Rips, Čech, etc.)
  • Filtration: determine filter functions (TF-IDF, word embeddings, topic models, sentiment, PCA, etc.), overlap of filter intervals, filter clustering methods and distance used for clustering.
  • Create a Persistence diagram (e.g. persistence barcode or graph) [18]
• Extract TDA features
• Classification / Clustering

ML and NLP Applications

The following are some relevant examples of TDA applications to machine learning and natural language processing:

1. Georges, 2019. Topological Based Machine Learning.
2. Elyasi & Moghadam, 2019. An Introduction to a New Text Classification and Visualization for Natural Language Processing Using Topological Data Analysis.
3. Islambekov & Gel, 2019. Unsupervised Space-Time Clustering Using Persistent Homology.
4. Savle, Zadrozny & Lee, 2019. Topological Data Analysis for Discourse Semantics?
5. Gholizadeh, Seyeditabari & Zadrozny, 2018. Topological Signature of 19th Century Novelists: Persistent Homology in Text Mining.
6. Pereira & de Mello, 2015. Persistent homology for time series and spatial data clustering.
7. Pereira & de Mello, 2014. Data Clustering Using Topological Features.
8. Zhu, 2013. Persistent Homology: An Introduction and a New Text Representation for Natural Language Processing.

Conclusion

Ultimately, the goal is to apply TDA as a tool and not delve into researching its feasibility for NLP tasks. This groundwork has already been done by others, who have shown its ability to extract various kinds of features that can be used for supervised or unsupervised learning.

The aim of applying TDA to misinformation detection is bifold: to gain better insight into the “shape” of fake news, and extract topological features for fake news detection. TDA offers a more holistic and insightful way to understand and visualise the fundamental characteristics of fake news. These characteristics can later be transformed into features for clustering or classification. Another advantage of using TDA is its greater robustness to noise and distortion as compared to traditional clustering.

References

[1] L. Parida, N. Haiminen, D. Haws, and J. Suchodolski, “Host trait prediction of metagenomic data for topology-based visualization,” 2015. doi:10.1007/978-3-319-14977-6_8.

[2] P. Y. Lum et al., “Extracting insights from the shape of complex data using topology,” 2013. doi:10.1038/srep01236.

[3] M. Feng and M. A. Porter, “Spatial Applications of Topological Data Analysis: Cities, Snowflakes, Random Structures, and Spiders Spinning Under the Influence,” 2020. arxiv.org/abs/2001.01872.

[4] F. A. Khasawneh, E. Munch, and J. A. Perea, “Chatter Classification in Turning using Machine Learning and Topological Data Analysis,” 2018. doi:10.1016/j.ifacol.2018.07.222.

[5] K. N. Ramamurthy, K. R. Varshney, and K. Mody, “Topological data analysis of decision boundaries with application to model selection,” 2019.

[6] G. Carlsson et al., “Topological Data Analysis and Machine Learning Theory,” 2012.

[7] C. M. M. Pereira and R. F. De Mello, “Persistent homology for time series and spatial data clustering,” 2015, doi:10.1016/j.eswa.2015.04.010.

[8] H. Edelsbrunner and D. Morozov, “Persistent homology: Theory and practice,” 2014. core.ac.uk/reader/268224700.

[9] G. Singh, F. Mémoli, and G. Carlsson, “Topological Methods for the Analysis of High Dimensional Data Sets and 3D Object Recognition,” 2007, doi:10.2312/SPBG/SPBG07/091-100.

[10] N. O. Attoh-Okine, “Big data and differential privacy: Analysis strategies for railway track engineering,” 2017.

[11] N. Elyasi and M. H. Moghadam, “An Introduction to a New Text Classification and Visualization for Natural Language Processing Using Topological Data Analysis,” 2019. arxiv.org/abs/1906.01726.

[12] A. E. Sizemore, J. E. Phillips-Cremins, R. Ghrist, and D. S. Bassett, “The importance of the whole: Topological data analysis for the network neuroscientist,” 2018. doi:10.1162/netn_a_00073.

[13] M. Saggar et al., “Towards a new approach to reveal dynamical organization of the brain using topological data analysis,” 2018. doi:10.1038/s41467-018-03664-4.

[14] I. R. Sami and K. Farrahi, “A simplified topological representation of text for local and global context,” 2017. doi:10.1145/3123266.3123330.

[15] J. Murugan and D. Robertson, “An Introduction to Topological Data Analysis for Physicists: From LGM to FRBs,” 2019. arxiv.org/abs/1904.11044.

[16] A. Bak, “Topological Data Analysis: How Ayasdi used TDA to Solve Complex Problems,” YouTube, 2013. youtube.com/watch?v=x3Hl85OBuc0

[17] M. Carrière, B. Michel, and S. Oudot, “Statistical analysis and parameter selection for mapper,” 2018.

[18] R. Ghrist, “Barcodes: The persistent topology of data,” 2008, doi:10.1090/S0273-0979-07-01191-3.

Header image from: [7] C. M. M. Pereira and R. F. De Mello, “Persistent homology for time series and spatial data clustering,” 2015, doi:10.1016/j.eswa.2015.04.010.